NEUACM 2025 Winter Training 2 题解

D 松鼠聚会

题意

二维平面上 $n$ 个点。求其中一个点使得其他点到该点的切比雪夫距离之和最小。

$0 \le n \le 10^5$。

分析

切比雪夫距离含有 $\max$，难以维护。考虑通过坐标变换

$\left[ \begin{matrix} x'\\ y'\\ \end{matrix} \right] = \frac{1}{2} \left[ \begin{matrix} 1 & 1\\ 1 & -1\\ \end{matrix} \right] \left[ \begin{matrix} x\\ y\\ \end{matrix} \right]$

将切比雪夫距离转化为曼哈顿距离求解。

对于点 $(x_i, y_i)$，其他点到该点的距离和为：

$\begin{align*} \text{dis}_i &= \sum_{j \ne i} |x_j - x_i| + |y_j - y_i|\\ &= \sum_{x_j < x_i} (x_i - x_j) + \sum_{x_j > x_i} (x_j - x_i) + \sum_{y_j < y_i} (y_i - y_j) + \sum_{y_j > y_i} (y_j - y_i) \end{align*}$

将坐标排序后计算即可。

E ABB

题意

求使给定小写字母字符串成为回文串需在字符串末尾加入字母的最少数量。

字符串长度 $\text{len} \le 4 \times 10 ^ 5$。

分析

当然可以用马拉车解决。但是没必要。

题意转化后其实就是找字符串中最长的回文后缀，后缀不够明了，可以反转后转化为找前缀。根据回文串的性质，回文串反转后不变。所以我们就是在反转后的串中寻找最长的前缀使得它等于反转前的后缀。这启发我们用 $\text{KMP}$ 算法求解，我们将反转后的字符串拼接到原字符串前，我们要找的就是 $\text{next}_{2n}$。但是有可能此时 $\text{next}_{2n} > n$，为了避免这种情况，我们在中间添加一个特殊字符即可。

H 图腾

题意

给定一个 $1 \sim N$ 的排列。

求满足

$1≤a<b<c<d≤N,y_a<y_c<y_b<y_d$

的四元组个数与满足

$1≤a<b<c<d≤N,y_a<y_b<y_d<y_c$

或

$1≤a<b<c<d≤N,y_a<y_d<y_c<y_b$

的四元组个数的差。

对于 $100\%$ 的数据，$N ≤ 200000$。

以下是两种四元组的图形。

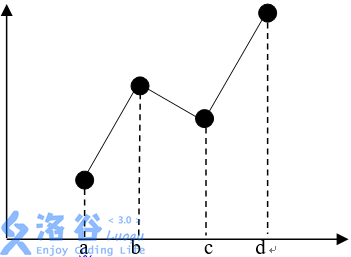
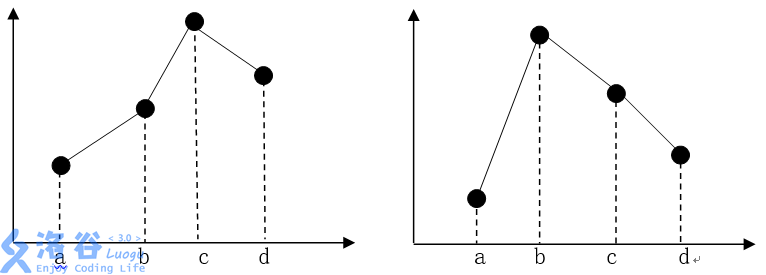
分析

每个四元组都难以单独计算，而问题要求我们算它们的差，所以，我们尝试用容斥把式子变形，消去不好算的部分。

定义 $[abcd]$ 表示符合相对大小关系四元组的数量。例如 $[1234]$ 表示单调递增的四元组的个数。

$\begin{align*} &[1324] - [1243] - [1432]\\ = &([13xx] - [1342]) - ([1x4x] - [1342]) - ([1x3x] - [1234])\\ = &[13xx] - [1x4x] - [1x3x] + [1234]\\ = &[13xx] - ([1xxx] - [1x2x]) + [1234]\\ = &[13xx] - [1xxx] + [1x2x] + [1234]\\ \end{align*}$

这个式子的推到还是很有技巧性的。我们发现通过两位去凑，总能消除一个共同的四元组。
比如如果你想要消去 $[1234]$，那么 $[1324] - [1243]$ 可以变形为 $([1xx4] - [1234]) - ([12xx] - [1234])$ 来消去。
多试几次消去不同的项就能凑出来。

到这里问题解决的一半，剩下难点在于如何计算每一项。

对于 $[1xxx]$ 和 $[1234]$ 还是很好计算的，这里不再赘述。

对于 $[1x2x]$，我们可以枚举 $2$ 出现的位置。

对于 $2$ 右边的 $x$ 容易处理，只需要乘上右边大于 $a_i$ 的个数。
左边相当于要求 $[132]$。并且此时我们只能枚举最右边 $2$ 的位置。

我们再次尝试容斥原理计算。我们发现，我们可以算出满足左边两个数至少存在一个小于 $a_i$ 的三元组个数为 $\tbinom{i - 1}{2} - \tbinom{G_i}{2}$，其中 $G_i$ 为左边大于 $a_i$ 的元素个数。
满足这样的三元组的和为 $[123] + [132] + [213] + [312]$。
其中 $[123]$ 很好算， $[213]$ 和 $[312]$ 可以就是求左边有多少个右端小于 $a_i$ 的“下降”，可以通过树状数组计算。

对于 $[13xx]$，我们发现将这个排列求逆后正好是 $[1x2x]$！我们只需要把原排列求逆再用 $[1x2x]$ 的方法计算即可。

I Triangle

题意

给出一个正整数 $S$ $( 1 \le S \le 10^{18} )$，你需要找出三个 $[0,10^9]$ 范围内的点。
使得构成的三角形面积是 $\displaystyle \frac{S}{2}$。

分析

可以固定一个一个点为 $(0, 0)$。剩下两个坐标为 $(x_1, y_2)$、$(x_2, y_2)$。

$S = \frac{1}{2}\left|\begin{matrix} x1 & y1 \\ x2 & y2 \\ \end{matrix}\right|$

我们让 $x1$、$y2$为 $\left\lceil\sqrt{S}\right\rceil$，调整 $x2$、$y1$，即可完成。

J Shift and Flip

给你两个 $\text{01}$ 串 $A$ 和 $B$，你可以进行以下 $3$ 种操作：

将 $A$ 左移一位（如 $\texttt{0011} \rightarrow \texttt{0110}$）。
将 $A$ 右移一位（如 $\texttt{0011} \rightarrow \texttt{1001}$）。
选择一个满足 $B_i = 1$ 的位置 $i$，令 $A_i = 1 - A_i$。

问要使 $A$ 和 $B$ 相等至少要进行几次操作。

$\text{len}_A, \text{len}_B \le 2000$。

分析

显然如果 $A$ 中有 $1$，而 $B$ 中没有 $1$，问题无解。

显然如果 $A$ 和 $B$ 中都没有 $1$，答案为 $0$。

下面我们只需要解决 $B$ 中至少有一个 $1$ 的情况。
通过简单分析，我们可以将整个过程总结为以下三步。1. 去往第一个小修改的位置；2. 沿着一个方向不断修改；3. 将 $A$ 和 $B$ 对齐。

我们可以想象有一个初始为 $0$ 计数器，当左移时计数器减 $1$，右移时计数器加 $1$。
我们定义整个过程中计数器的最小值为 $l$，最大值为 $r$，最后的值为 $d$。
根据我们刚才的分析，整个过程要么是“左右左”，要么是“右左右”，那么整个移动的距离就是 $2 \times (R - L) - \left|d\right|$。

下面我们不妨设过程为“左右左”来解决，对于“右左右”我们可以将 $A$ 和 $B$ 反转后用相同的方法解决。

我们先预处理出 $\text{pre}_i$ 和 $\text{suf}_i$ 分别表示 $B$ 中 $i$ 左边和右边第一个 $1$ 与 $i$ 的距离。
然后我们可以枚举 $d$，来确定 $l$ 和 $r$。
我们扫描 $A$ 串，若 $A_i \ne B_{(i + d) \bmod n}$ 则说明该位置要反转。
若 $\text{pre}_{(i + d) \bmod n} \le d$，则说明我们可以在右移的过程中某个位置将这一位修改。
否则，说明我们需要在一开始多左移或右移几位来修改这一位。

如果要通过左移修改，那么要满足 $\displaystyle -l \ge \text{pre}_i$；

如果要通过右移修改，那么要满足 $\displaystyle r \ge d + \text{pre}_{(i + d) \bmod n}$。

这样我们就有了若干个约束条件，优化的目标是让 $r - l$ 尽可能小。
我们通过图像来解决这个最优化问题。我们将所有的条件画在坐标系中，发现是若干 $\displaystyle \frac{3}{4}$ 平面交。
我们可以排序后用单调栈保留相交后最外边的 $\displaystyle \frac{3}{4}$ 平面，在交点处求解。

复杂度 $\mathcal{O}(n^2 \log n)$。如果用桶排可以优化到 $\mathcal{O}(n^2)$。