NEUACM 2025 Winter Training 3 题解
B「TAOI-3」终有一天,飞向水平线的彼方
题意
原题链接:https://oier.team/problems/X8C。
Mio 有一个长度为 $n$ 的正整数数列 $a_1, \ldots, a_n$。她会对这个序列进行若干次操作,每次她会选择一对正整数 $l,r$,满足 $1 \le l \le r \le n$,且 $(r-l+1)$ 为偶数,然后进行以下两种操作中的一种:
- 对于所有整数 $i \in [l,r]$,令 $a_i \gets a_i+\left(|i-\frac{r+l}{2}|+\frac{1}{2}\right)$。
- 对于所有整数 $i \in [l,r]$,令 $a_i \gets a_i-\left(|i-\frac{r+l}{2}|+\frac{1}{2}\right)$。
形象化地,你可以把这理解为,选择某区间内最中间的数作为中轴,然后把区间内的所有数加上或减去它与中轴的距离。例如,如果选择 $l=1$,$r=8$,效果就是把数列的前 $8$ 个数分别加上或减去 $4,3,2,1,1,2,3,4$。
在 Mio 的操作中,她希望任意时刻数列里的所有数都是正整数。
现在,Mio 想要知道,能否用这样的操作把数列 $a_1, \ldots, a_n$ 变成目标正整数数列 $b_1, \ldots, b_n$。
对于所有数据,保证 $1 \le T \le 5$,$1 \le n \le 10^5$,$1 \le a_i,b_i \le 10^9$。
分析
首先非负是不用考虑的,可以先做完所有的加操作再做减操作。
然后我们注意到所有的 $r - l + 1 > 2$ 的操作都可以分解为一些 $r - l + 1 = 2$ 的操作。因为原先的操作是一个“凹”的形状,可以看作是一整块减去一个“凸”的形状,而“凸”的形状是可以用 $r - l + 1 = 2$ 的操作拼出来的。
那么我们的做法就显然了,只需要从左到右把 $[1, n)$ 范围内的数通过 $r - l + 1 = 2$ 的操作变成我们需要的数再看最后面的数有没有变成我们要的数。
G 超立方体
题意
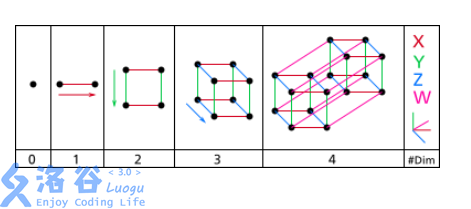
$D$ 维空间内的超立方图有 $2^D$ 个点,我们把这些点从 $0$ 到 $2^D-1$ 依次编号。
有一个有趣而重要的充要结论是:一定存在一种编号的方式,使得图中任意两个有边相连的顶点的编号的 $2$ 进制码中,恰好有一位不同。
在2维和3维空间内这个结论可以这样形象的理解:对于 $2$ 维空间,我们只要把这个正方形放到第一象限内,使得 $4$ 个顶点的坐标按逆时针顺序依次为 $(0,0),(1,0),(1,1),(0,1)$,然后再把坐标看成 2 位 2 进制数,依次将这 4 个点编号为 $0,1,3,2$ 即可。
对于 $3$ 维空间,同样我们可以将立方体的一个顶点与原点重合,并使得所有棱均平行于坐标轴,然后分别确定这 $8$ 个点的坐标,最后把 $3$ 维空间内的坐标看成一个 $3$ 位 $2$ 进制数即可。对于 $D$ 维空间,以此类推。
现在对于一个 $N$ 个点 $M$ 条边的无向图(每个点从 $0$ 到 $N-1$ 编号),Will 希望知道这个图是否同构于一个超立方图。
$Q~\leq~3,~N~\leq~32768,~M~\leq~1000000$
分析
对于一个 $D$ 维的超立方体,点数 $n = 2 ^ D$,边数 $\displaystyle m = \frac{nD}{2} = \frac{D 2^D}{2}$。我们可以先用以上公式简单判断。
具体如何判断,我们可以发现原点的选取是任意的,维度的顺序也是任意的。所以,我们可以尝试把某一维度的边全部删去,将超立方体划分成两个不连通的 $D - 1$ 维超立方体,然后递归判断。
具体来说,任选一条边断开,将两个点分别放入 $A$ 和 $B$ 两个集合。我们从 $B$ 中选择未配对的点 $p$ 与 $A$ 集合中的点配对,即看点 $p$ 是否有边与 $A$ 中的点相连,若有且仅有一条,那么这一对点就配对了。假设配对的点为 $q$,根据超立方体的性质,一个点有且仅有一个配对点,那么剩下的相连的点就是属于各自集合的了。也就是把与 $p$ 相连的其他点放入 $B$,与 $q$ 相连的其他点放入 $A$。如果不存在这样的点或者存在不止一个,那么说明这个图不是超立方体。这样不断重复就将整个超立方体分成了两个规模较小的超立方体,递归判断。
J Erasing Vertices
题意
给定一个点数为 $n$ $(1 \le n \le 100)$ 的有向图。
等概率随机选定一个还未删除的点 $x$,删除 $x$ 以及图中 $x$ 能通过某些路径到达的点(指向这些点的边也会被删除)。如果图中没有任何未被删除的点,则结束操作,否则重复此操作。
求期望做多少次操作(与标准答案的误差不超过 $10^{−9}$)。
分析
假设随机变量 $X_i$ 表示操作完后点 $i$ 是否被选中过。那么,我们所求的就是 $\displaystyle E (\sum X_i)$。
难点在于如何求 $P(X_i)$。
首先我们可以发现如果一个点 $j$ 无法到达 $i$,那么 $j$ 是否选取与 $i$ 无关。也就是说 $P_i$ 只与能够到达 $i$ 点有关。这个问题可以看作 $n$ 个球,其中有一个球 $i$,$m$ 个 “重要” 的球,剩下的是无关的球。每次从中抽取一个,若是无关的球则接着抽取。求最后抽到 $i$ 的概率。这里 “重要的球” 就相当于可以到达 $i$ 的点。我们稍加分析就能够得出 $P(X_i) = \displaystyle \frac{1}{m + 1}$,其中 $m$ 是可以除开 $i$ 自己外可以到达 $i$ 的点的数量。
知道了这个结论剩下的就是求可以到达 $i$ 的点的数量,可以 $\text{BFS}$ 或者传递闭包解决。
K Tree Edges XOR
题意
给定一棵 $n$ 个结点的树,保证 $n$ 是奇数,边有边权 $w_{i,1}$。现在你可以任意次把与一个边相连的其他边的权值异或上这条边的权值,求是否可以让每条边的边权变为 $w_{i,2}$。
$n \le 10^5$,$w \le 2^{30}$。
分析
本题突破口:化边权为点权,使得某条边的边权为连接的点的点权异或。
我们发现这样转化后,操作相当于交换两个点的点权。
我们令根点权为 $0$,算出其他点的点权,然后就是要判断能否转化。由于我们的根的点权钦定为 $0$,所以不能直接比较两个集合是否相同。我们发现,如果此时我们改变根的点权为 $x$,那么其他点的变化就是异或上 $x$。假设此时点权为 $a_i$,期望是 $b_i$,我们就是要判断是否存在一个 $x$,使得集合 $\{a_i \oplus x\} = \{b_i\}$
由于 $n$ 为奇数,所以我们可以通过 $\oplus_{i \le n} (a_i \oplus x) = x \oplus_{i \le n} a_i = \oplus_{i \le n} b_i$ 来解出 $x$。然后带入回去判断集合是否相等。
L Bitwise Slides
题意
给定一个长度为 $n$ $(n \le 10^5)$ 序列 $a_i$,三个初始为 $0$ 变量 $P$、$Q$ 和 $R$,从左到右遍历序列,每一要选一个变量异或当前的数,要求任意时刻三个变量不可以两两不同。问合法方案数。
分析
定义异或前缀和 $\text{pre}_i = \oplus_{j \le i} a_j$。那么任意时刻有 $P \oplus Q \oplus R = \text{pre}_i$。并且由于任意时刻三个变量不可以两两不同,那么至少有两个变量相同,而相同的变量异或为 $0$,说明至少有一个变量为 $\text{pre}_i$ 且剩下两个变量相同。
定义状态 $f_{i, x}$ 表示操作完前 $i$ 个数,另外两个数为 $x$ 的方案数。
我们不妨设这三个数为 $(x, x, y)$,说明 $y = \text{pre}_i$,那么这三个数只有可能从 $(x, x, z)$ 或 $(x, y, y)$ 转变而来。对于前者 $z = \text{pre}_{i - 1}$,有转移 $f_{i,x} = f_{i - 1, x}$。对于后者,说明 $x = \text{pre}_{i - 1}$,有转移 $f_{i, x} = 2 \times f_{i - 1, y}$。此外,还有一个细节是 $z = x$ 时,也就是 $x = \text{pre}_{i - 1}$,第一个转移应该是 $f_{i,x} = 3 \times f_{i - 1, x}$
综上我们发现,只有在 $x = \text{pre}_{i - 1}$ 时,转移比较特殊,其他情况下,都是复制上一状态。所以我们可以用 $\text{std::map}$ 来存储状态,每次只更更新 $x = \text{pre}_{i - 1}$ 的状态。
答案就是 $\text{std::map}$ 中元素的和。

